文章信息
- 张鹏宇, 刘恩顺, 何易
- ZHANG Peng-yu, LIU En-shun, HE Yi
- 基于均值分析法改良的中药处方信息无量纲化方法探讨
- Discussion on the method of Non-dimensionalization of traditional Chinese medicine prescription information based on mea value analysis
- 天津中医药, 2016, 33(12): 760-762
- Tianjin Journal of Traditional Chinese Medicine, 2016, 33(12): 760-762
- http://dx.doi.org/10.11656/j.issn.1672-1519.2016.12.14
-
文章历史
- 收稿日期: 2016-07-26
2. 天津中医药大学第二附属医院, 天津 300150
辨证论治集中体现了中医个体化诊疗的临床特点,其过程涵盖了从认识疾病、把握证候,到确立治法、处方遣药的全过程。中药处方是最终体现“理、法、方、药”的系统运用和辨证论治水平的关键环节[1],药味选择和药量加减是处方变化的主要内容,它不仅要关注疾病的个体化特征,也充分考虑疾病总体规律,具有高度灵活性。在对中医辨证论治的疗效进行评价时,一方面,患者大量的个体化治疗信息闲置,未能得到充分利用;而另一方面,中药处方的效果不能得到客观证实,制约着中医药在临床实践中的应用。因此,如何进行中药处方信息量化,使其得到充分合理运用,进而合理评价中医药疗效,成为促进中医不断发展的过程中亟待解决的问题[2-3]。
笔者在分析当前中药处方信息量化方法的基础上,提出建立一种充分利用个体化治疗信息的方药量化评价方法的构建思路,现从两方面分述如下。
1 当前中药处方信息量化方法不能满足合理评价中医药疗效的需要十余年来,不断有学者认识到进行中药处方信息量化的必要性,并提出了量化的思路与方法,其中代表性较强的有差值分析法、均值分析法、归一化区间参数法及非线性函数法等[4-11],其基本思路均为建立以相对药量为基础的数学模型[12-14]。
由于不同药物的常规使用剂量往往具有较大差异,即使其用量相同,在处方中发挥的作用也各有差异,因而各药物的实际用量不适合进行直接比较,需引入相对药量的概念,以《中华人民共和国药典》提示的各中药常规剂量为依据进行计算分析[15],对各药物进行重新量化,使方剂中的不同中药具备统一的可比基础。
1.1 差值分析法差值分析法是指通过中药处方中出现药物的实际用量与其最大、最小常规用量差值的比值来分析处方药量强度的方法,将药量强度的权重设为k,如模型1所示。其中m为常规用量的下限,M为常规用量的上限,x为实际用量[16]。(常规用量依据《中华人民共和国药典》提示)
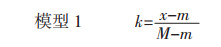 |
该方法可以快速计算分析出方剂中各药物剂量相对于其常规用量的使用情况,其不足在于,若x < m,则k为负值;若x=m,则k固定为0;若x=M,则k固定为1,即无法反映实际用量等于其常规用量端点值的药物的使用强度差异。
1.2 均值分析法均值分析法是通过药物的实际用量与其最大、最小常规用量均值的比值来分析药量强度的方法,将药量强度设为k,如模型2所示。其中m为常规用量的下限,M为常规用量的上限,x为实际用量[16]。(常规用量依据《中华人民共和国药典》提示)
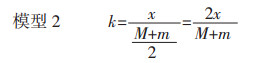 |
该方法不仅反映了药物实际用量与其常规用量的关系,显示了相对药量,且k的取值总是大于0,在实际用量与常规用量的各种大小关系下其值均有意义,并方便计算。
1.3 归一化区间参数法归一化区间参数法亦为通过比较药物实际用量与常规用量大小关系来分析其作用强度的方法,与上述方法的主要区别在于将药物的相对药量归一化到某一固定的区间内。将相对药量设为G,如模型3所示。其中a为常规用量的下限,b为常规用量的上限,x为实际用量,m为归一化区间参数(设为50);n为归一化下限(设为10)[17]。
 |
(m=50,n=10)
该模型部分采用了差值分析的方法,因而亦存在与差值分析法相似的不足,即所有实际用量等于其最小常规用量的药物,作用强度均为n;所有实际用量等于其最大常规用量的药物,作用强度均为m+n。而且该归一化区间参数及归一化下限均是人为设定的固定常数,可能不具有对于不同药物的普适性[18]。
1.4 非线性函数法在上述模型中,药物的实际用量与其作用强度均为线性关系,很可能与临床用药实际情况不符,故而有学者提出建立非线性函数模型,以合理反映药物的量效关系的方法[19]。将药量强度的权重设为X,如模型4所示。其中m为常规用量的下限,M为常规用量的上限,x为实际用量,k=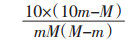
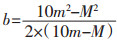
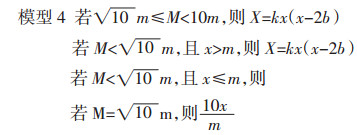 |
该方法考虑了药物用量与作用强度的非线性关系,具有一定合理性,但其以二次函数为基础建立模型,虽然模拟了药物量效间存在非线性关系的情况,却因二次函数自身具有一定的固定特点而难以说明量效关系是否可用二次函数表示。
以上方法以分析相对药量为基本思路建立了不同的数学模型,但仅考虑了药量对单味药作用的影响,未提出如何据此分析处方整体的作用。故而现有的中药处方信息量化方法不能完全满足合理评价中医药疗效的需求,需要进行进一步的探索。
2 以均值分析法为基础的中药处方信息量化方法结合此前学者的研究,笔者认为引入相对药量对于合理评价药物及处方的作用是必不可少的。综合考虑以上各种方法的优势与不足,发现均值分析法具有简便有效且人为干预因素较少的特点,故现以均值分析法即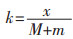
设一张所含药味数为n的处方的综合作用为T,药物实际用量为x,相对药量为k。其中k=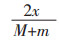
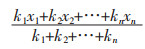
相对药量k反映某药物实际用量在其常规用量中所处的位置,将方中每一味药物的k值相加,即为整张处方的相对药量(k1+k2+...kn)。用某一味药物i的相对药量与整张处方的相对药量作比,可得该药物在处方中所占的比重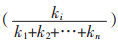
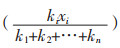
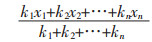
对于任一处方,每味药物在处方中的占比之和均为1,故而即使是所含药味数不同的处方亦具有均衡的可比基础;同时又引入相对药量解决了常规用量不同的药物的比较问题,因此,该模型综合反映了药味、药量两方面的信息,避免了“方中药味越多,处方作用越强”与“实际用量越大,药物作用越强”两方面的错误,可以较为合理地评价中药处方的综合疗效。
但是,由于通过该模型无法对处方是否对证进行判断,故而该模型适用于同时比较若干具有共同特征(如针对相同疾病或证候)的处方,而不能解决所有处方的比较问题;并且仅将药物实际用量与常规用量上下限的均值作比亦存在一定问题,因为可能存在某些药物的常规用量上下限数值不一致而均值一致,该模型下,若这些药物实际用量相同则所得相对药量相同,但临床实际可能并非如此。这些问题需要进一步探索以解决。
总之,本研究在分析目前中药处方信息量化现 状的基础上,针对中药处方的疗效量化提出了具体 的研究思路与方法,希望有益于中医药疗效的合理 评价,促进中医药疗法的临床应用。
| [1] | 雍小嘉.采用知识发现技术判断方剂功效的方法研究[D].成都中医药大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10633-2006170530.htm |
| [2] | 李小梅, 李续娥, 郭宝江. 数学方法在中医药研究中的应用[J]. 中华中医药学刊, 2007, 10 : 2103–2104. |
| [3] | 杨松涛, 王键. 略论中医药学研究中的数学量化方法[J]. 中国中医基础医学杂志, 2009, 15 (4) : 314–315. |
| [4] | 高全泉, 任廷革, 刘晓峰, 等. 中医方剂药物相对药量改进计算模型[J]. 海南师范大学学报(自然科学版), 2008, 21 (4) : 362–366. |
| [5] | 顾作林, 袁同山, 李芳, 等. 中医方药量化研究中"相对药量"的数学模型体系[J]. 数学的实践余认识, 2010, 40 (9) : 154–157. |
| [6] | 肖二刚.伤寒论方剂数字化研究计算机辅助分析[D].天津:天津中医药大学, 2009. |
| [7] | 王文刚. 基于量效的方剂分析法尝试[J]. 陕西中医学院学报, 2011, 34 (6) : 74–74. |
| [8] | 周铭心, 张学良, 李程. 复诊处方用药加减与剂量变化分析方法及指标设计[J]. 新疆中医药, 2012, 32 (4) : 1–6. |
| [9] | 杨斌.方剂处方法的宏观量化分析方法研究与实践[D].北京:北京中医药大学, 2002. http://cdmd.cnki.com.cn/Article/CDMD-10026-2002081981.htm |
| [10] | 刘晓峰, 任廷革, 高全泉, 等. 中医方剂功效定性和定量研究再探[J]. 中国中医药信息杂志, 2009, 16 (1) : 92–95. |
| [11] | 白春清. 计量辨证和量化组方数理模型初探[J]. 湖北中医学院学报, 2006, 7 (1) : 57–59. |
| [12] | 张治中.国医大师临证处方用药剂量方剂计量学分析[D].乌鲁木齐:新疆医科大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10760-1013360308.htm |
| [13] | 康琳.数学方法在中医药学研究中的应用[D].石家庄:河北科技大学, 2014. |
| [14] | 唐慧勤, 王勤, 卢凤来, 等. 数学模型在中医药研究中的应用与思考[J]. 中成药, 2013, 36 (4) : 804–806. |
| [15] | 董翠新, 严兴海, 李军, 等. 何复东临证方剂计量研究[J]. 中医药通报, 2016, 15 (2) : 43–46, 48. |
| [16] | 刘霞, 张砚, 李晓伟, 等. 方剂量化的数学分析方法研究[J]. 天津中医药大学学报, 2012, 31 (4) : 244–246. |
| [17] | 胡波.中药方剂性味的多维宏观量化表达方法研究[D].成都:成都中医药大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10633-2005122204.htm |
| [18] | 徐培平.方药配伍的"耦合"效用及其组方规律研究的方法学探讨[D].广州:广州中医药大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10572-2008099990.htm |
| [19] | 顾作林, 李芳, 刘东艳, 等. 基于突变理论的中药"相对峰值"概念的提出及其模型建立[J]. 数学的实践与认识, 2015, 45 (5) : 102–106. |
2. The Second Affiliated Hospital of Tianjin University of Traditional Chinese Medicine, Tianjin 300150, China
 2016, Vol. 33
2016, Vol. 33